A Few Useful Things To Know About Machine Learning

One of the deep, dark secrets of machine learning is that beneath all of the math, statistics, and algorithms, there's sort of a "black art" to actually building useful models. I think the reason for this stems primarily from the counter-intuitiveness of working in high-dimensional spaces coupled with a tendancy to focus on things that can be explicitly defined and measured (such as a new algorithm) rather than more subjective nuances like developing features based on domain-specific knowledge. While the former is interesting and necessary to advance the state of the art, the latter is more likely to have a significant impact on most real-world projects. It is both very helpful and somewhat difficult to find practical lessons in machine learning that are well-articulated and based on sound principles.

One resource I've come across that is incredibly useful in this regard is Pedro Domingos' "A Few Useful Things to Know about Machine Learning" (link), from which the title of this blog post was unabashedly stolen. The paper is a survey of helpful reminders about the nature of the problems one deals with when designing predictive models, and practical guidelines for overcoming them. The remainder of this post is dedicated to distilling these reminders down to their essence for quick reference. However, I would encourage the interested reader to explore the full paper in depth.

Learning = Representation + Evaluation + Optimization

There's a huge variety of learning algorithms out there with more being published all the time. However it's important to realize that any supervised learning algorithm can be reduced to three components:

Representation - The hypothesis space of the learner. Equates to the way in which a model is defined. For example, k-nearest neighbor uses an instance-based representation while a decision tree is represented by the set of branches forming the tree.

Evaluation - The objective or scoring function used to distinguish good models from bad models. This might be accuracy, f1 score, squared error, information gain, or something entirely different.

Optimization - The method used to search among the set of possible models allowed by the representation (i.e. the hypothesis space) to find the "best" model (as defined by the evaluation function). Many algorithms with convex search spaces use some form of gradient descent, for example.

The selection of these three categories defines the set of possible models that can be learned, what the "best" model looks like, and how to search for that model.

It's Generalization That Counts

The fundamental goal of machine learning is to build a model that generalizes well. It's easy to build a model that learns the training data exceptionally well but performs miserably on new data. This is why cross-validation is so important - without evaluating a model on data not seen during training, there's no way to tell how good it actually is. Even when using cross-validation properly, it's still possible to screw this up. The most common way is overtuning hyper-parameters. This will appear to be improving the model's performance on test data but could actually harm generalization if taken too far.

Data Alone Is Not Enough

There's no free lunch in machine learning - any learner must have some form of domain knowledge provided to it in order to perform well (this can take many forms and depends on the choice of representation). Even very general assumptions, such as similar examples having similar classes, will often do very well. However, much more specific assumptions will often do much better. This is because induction is capable of turning a small amount of input knowledge into a large amount of output knowledge. One may think of learning in this context as analogous to farming. Just as farmers combine seeds with nutrients to grow crops, learners combine knowledge with data to grow models.

Overfitting Has Many Faces

Overfitting is a common problem in machine learning where a learner tends to model random sampling noise in the data and ends up not generalizing well. Overfitting is usually decomposed into bias and variance. Bias is the tendency to consistently learn the wrong thing. Variance is the tendency to learn random things that don't model the true function. The below graphic, taken from Domingos' paper cited earlier, is a great illustration of these principles.

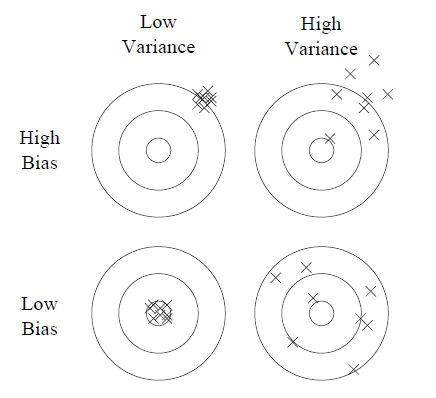
Source: "A Few Useful Things to Know about Machine Learning", Pedro Domingos

On some problems it is possible to get both low bias and low variance, but not always. Because learning algorithms often involve tradeoffs between bias and variance, it is sometimes true that simpler and less expressive algorithms like linear models may perform better than more powerful algorithms like decision trees. In general, the more powerful a learner is, the more likely it is to exhibit low bias but high variance. In these situations, the tendency to overfit must be counter-balanced with good cross-validation and adding a regularization term to the scoring function.

Intuition Fails In High Dimensions

The second big challenge after overfitting is often called the curse of dimensionality. Roughly speaking, as the number of features in a data set increases it becomes exponentially more difficult to train a model that generalizes well because the data set represents a tiny fraction of the total input space. Even worse, similarity measures fail to effectively discriminate between examples in high dimensions because at very high dimensions everything looks alike. This particular insight highlights the general observation that our intuition fails very badly in high dimensions because our tendency is to draw comparisions to what we know (i.e. three-dimensional space) when such comparisions are not appropriate. The lesson here is to be very cautious about adding features recklessly. Additionally, employing good feature selection techniques is probably very important to building a model that generalizes well.

Feature Engineering Is The Key

The choice of features used for a project is easily the biggest factor in its success or failure. Raw data (even cleaned and scrubbed data) is often not in a form that's amenable to learning. Aside from gathering data, designing features may be the most time-consuming part of any machine learning project. Because feature engineering usually requires some amount of domain knowledge specific to the problem at hand, it is very difficult to automate. This is also why algorithms that are good at incorporating domain knowledge are often the most useful.

One may be tempted to try lots of different features and evaluate their impact by measuring their correlation to the target variable, however the assumption that correlation to the target is a proxy for usefulness is false. The classic example here is the XOR problem. Two booleans measured independently against a target that is the exclusive-or of the dependent variables will have no correlation to the target, however taken together they provide a perfect decision boundary. The lesson is that feature engineering and feature selection typically cannot be automated by software, but may have a disproportionate effect on the project's outcome, so don't neglect them.

More Data Beats A Cleverer Algorithm

When faced with the challenge of overcoming a model performance bottleneck there are two fundamental choices - use a more powerful learning algorithm or get more data (either number of examples or additional features). Although the former is tempting, it turns out that the latter is often more pragmatic. Generally speaking, a simple algorithm with lots of data will beat a much more powerful algorithm with much less data. In some cases it may be possible to use a powerful algorithm with lots and lots of data, but often this problem is still computationally intractable, although there is significant and rapid progress being made in this area.

Another potential benefit of simple algorithms is that the learned model may be interpretable by human beings whereas a complex model is usually very opaque. There is a trade-off, however, in that a simple algorithm may not have sufficient expressiveness or depth in its representation model to learn the true function. Some representations are exponentially more compact than others for certain functions, and a function that may be easy for complex algorithms to learn may be intractable or completely impossible for simple algorithms to learn.